METODOS DE UN PASO
Los métodos de un paso son un conjunto de algoritmos para resolver ecuaciones diferenciales en un solo paso. Estos incluyen:
1. Método de Euler: este es un método simple que aproxima la solución al usar tangentes para estimar la pendiente de la curva en cada punto. Es fácil de implementar pero no es muy preciso.
2. Método de Runge-Kutta de segundo orden: este es un método más preciso que el Método de Euler. En este método, se utiliza el promedio de dos pendientes para aproximar la solución en cada punto.
3. Método de Runge-Kutta de cuarto orden: este es uno de los métodos más precisos que se pueden usar para resolver ecuaciones diferenciales. Utiliza una serie de cálculos para estimar la solución en cada punto y se utiliza en muchas aplicaciones prácticas.
4. Método de Adams-Bashforth: este es un método de múltiples pasos que usa estimaciones anteriores de la solución para calcular la próxima estimación. Es más preciso que el Método de Euler pero menos preciso que los métodos de Runge-Kutta.
5. Método de Adams-Moulton: este es otro método de múltiples pasos que utiliza la estimación inicial del Método de Euler, pero luego utiliza una fórmula más precisa para calcular la siguiente estimación. Es más preciso que el Método de Adams-Bashforth.
En general, los métodos de un paso son fáciles de implementar y pueden ser precisos si se selecciona el método adecuado para la ecuación diferencial en cuestión.
METODO DE PASOS MULTIPLES
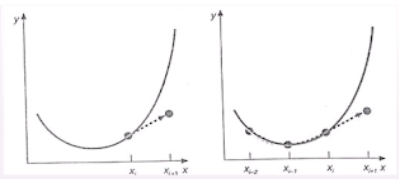
Los métodos de un paso descritos en las secciones anteriores utilizan información en un solo punto xi para predecir un valor de la variable dependiente yi+1 en un punto futuro xi+1. Procedimientos alternativos, llamados métodos multipaso, se basan en el conocimiento de que una vez empezado el cálculo, se tiene información valiosa de los puntos anteriores y esta a nuestra disposición. La curvatura de las líneas que conectan esos valores previos proporciona información con respecto a la trayectoria de la solución. Los métodos multipaso que exploraremos aprovechan esta información para resolver las EDO. Antes de describir las versiones de orden superior, presentaremos un método simple de segundo orden que sirve para demostrar las características generales de los procedimientos multipaso.
Esto lo podemos demostrar mediante las siguientes graficas.
SISTEMAS DE ECUACIONES DIFERENCIALES ORDINARIAS
APLICACIONES
Para aplicar métodos matemáticos a un problema físico o de la “vida real”, debemos formular el problema en términos matemáticos; es decir, debemos construir un modelo matemático para el problema. Muchos problemas físicos se refieren a las relaciones entre cantidades cambiantes. Dado que las tasas de cambio están representadas matemáticamente por derivados, los modelos matemáticos a menudo involucran ecuaciones que relacionan una función desconocida y una o más de sus derivadas. Tales ecuaciones son ecuaciones diferenciales. Ellos son el tema de este libro.
Gran parte del cálculo se dedica a aprender técnicas matemáticas que se aplican en cursos posteriores de matemáticas y ciencias; no tendrías tiempo de aprender mucho cálculo si insistes en ver una aplicación específica de cada tema tratado en el curso. De igual manera, gran parte de este libro está dedicado a métodos que se pueden aplicar en cursos posteriores. Sólo una parte relativamente pequeña del libro está dedicada a la derivación de ecuaciones diferenciales específicas a partir de modelos matemáticos, o relacionar las ecuaciones diferenciales que estudiamos con aplicaciones específicas. En esta sección mencionamos algunas aplicaciones de este tipo. El modelo matemático para un problema aplicado es casi siempre más sencillo que la situación real que se estudia, ya que generalmente se requieren supuestos simplificadores para obtener un problema matemático que pueda resolverse. Por ejemplo, al modelar el movimiento de un objeto que cae, podríamos descuidar la resistencia al aire y la atracción gravitacional de cuerpos celestes distintos de la Tierra, o al modelar el crecimiento de la población podríamos suponer que la población crece continuamente en lugar de en pasos discretos.









No hay comentarios.:
Publicar un comentario